HOW TO THINK LIKE A SPHERE
PLATONIC SOLIDS AS SPHERES
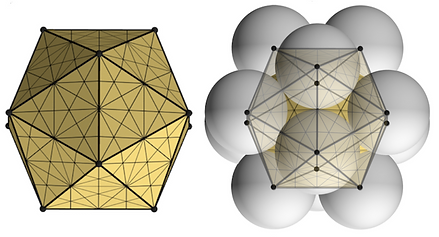
Icosahedron
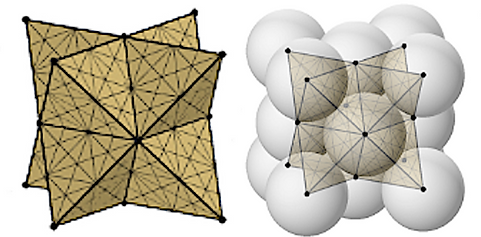
Duo-Tet Cube
Dodecahedron

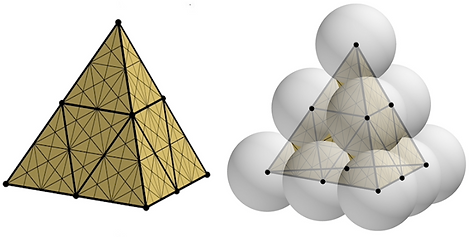
Tetrahedron
Octahedron

VE (Vector Equilibrium)

Victor Acevedo Media
The communication networks between the centers of the spheres define these geometrical systems. I include the VE with the 5 Platonic Solids because of its role as the beginning and end of our structural order.
To Think Like a Sphere Begin By Thinking Like a Circle
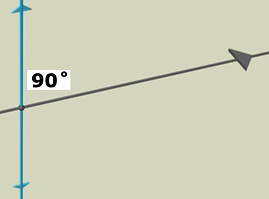
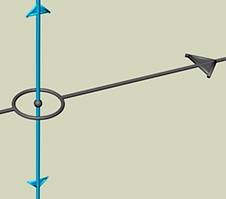
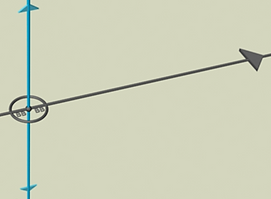
Our measuring system grows out of the communication networks that interconnect the centers of the closest packed same-sized spheres. The first word spoken in 'sphere-speak' was circle. A circle is the equator of a sphere. For both of them to exist physically there needs to be a location on a time line that begins measurement by 'remembering' 90˚. This generalized state need the special case, a BB, bellybutton.
Like our navel is the cut-off knot from all genetics before and a symbol of our independent existence, BB is the cut-off number from all measurement before and is the start of a new method for the measurement of structure. All measurement in Newtools geometry is relative to BB which becomes our scale number.
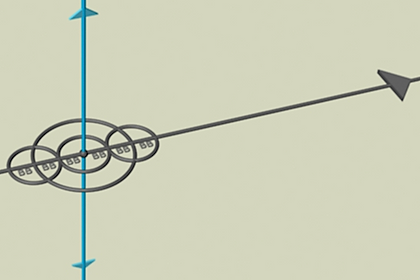
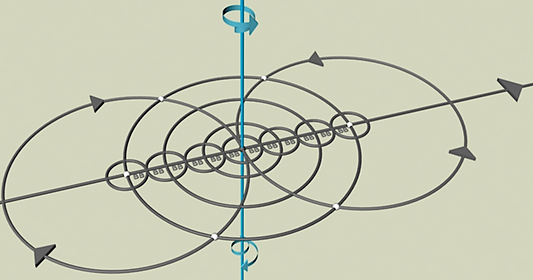
We use Buckminster Fuller's theory of the closest-packed state. He stated that three layers of spheres around the central sphere defines the first cycle of spherical growth. If BB is our scale number then the maximum reach of the center is 6 radii or 6BB. Once that limit is reached an axis of spin begins and we now have the 'two hands' of spin, clockwise/counter clockwise. An axis of spin will be used to align geometrical systems for 'compare and contrast' study. Four 6BB circles begin to spin around the center and achieve 60˚ orientation to each other. A 6BB radius sphere is born defining the 14-sided VE.
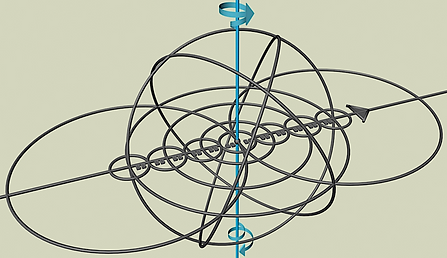
The 6BB VE becomes the push-off-start for Newtools geometry's structural order. From our original center order bursts out in "all-directions-all-at-once". Go to the Mapping portal for details.

You/Me BB Measuring System
You/Me Ball

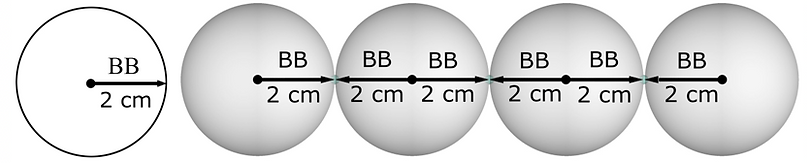
The purpose of this measuring system is to interconnect the "Not-Us" constants found in Design-in-Nature with you and me as local observers. To do that we need to choose a sphere to be our You/Me Ball.
In 2000, the International Table Tennis Federation changed the size of regulation ping pong balls from a radius of 1.9 cm (centimeters) to 2 cm. I had been purchasing ping pong balls to build models of Fuller's theories about the closest packing of same-sized spheres. When I discovered the change a 'lightbulb' went off in my imagination and this measuring system was born. The 2 cm radius lent itself much easier as a scale number, 6 BB = 12 cm. The idea of a BB scale number was born. Fuller had called this original sphere the Me Ball, I expanded it to include both you and me so we could be one local observer.
We now have a shared scale number, BB = 2 cm and we share a location-in-common, the center of this sphere. Every geometrical system, every measurement will now be relative to these two initial conditions of our You/Me Ball.
When you measure distance with spheres you always measure center-of-sphere to center-of-sphere. 6BB is the maximum limit of influence of our shared center. Any number larger will be relative to 6BB.
Closest-Packing of Same-Sized Spheres

You/Me Ball


Our You/Me Ball with radius of BB = 2 cm and the 4 circles that interconnect the center to the outside corners.
1st Layer
Maximum Radius of the Center = 2BB = 4 cm



The closest packing of spheres begins with asking a question,"What is the most effective minimum number of same-sized spheres needed to completely surround the You/Me Ball in a single layer? The answer will always be 12 same-sized spheres around one. The distance from the center to the centers of the 1st layer of spheres is 2BB = 4 cm. The first layer will always have a total of 13 spheres.
2nd Layer
Maximum Radius of the Center = 4BB = 8cm


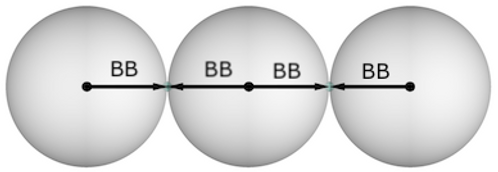
The second layer of same-sized spheres has 42 around 12 around 1. The 'sphere of influence' of the center of this amalgamation is 4BB = 8 cm. The second layer will always have a total of 54 spheres around 1.
3rd Layer
Maximum Radius of the Center = 6BB = 12cm


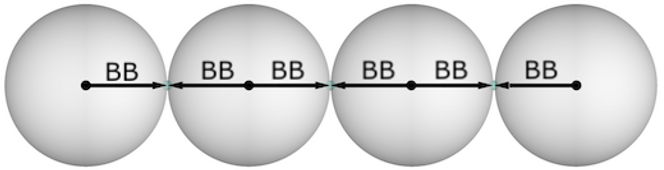
The third layer will have 92 same-sized spheres around 42 around 12 around 1. This maximum sphere of influence will always have 146 spheres around our central You/Me Ball. The maximum measurement is 6BB = 12 cm.


Dividing the whole in half reveals the hexagonal equator. We have been exploring the language of the spheres as a tool in your exploration of fundamental structure. The language of the 60˚triangle is the same language with a different dialect. The 6BB maximum limit can express itself in all of these forms. When you see a circle think hexagon. When you think of closest-packed spheres think of the family of shapes that grow from the 60˚triangle. The simplest expression of Design-in-Nature is based on a variety of options to utilize the efficiency of the MEM (Most Effective Minimum) state.
Basic Structural Job Descriptions Began as Spheres
We learned earlier that fundamental structure has two main job descriptions. The Sphere family (allspace-filling) has the ability, when stacked together, to fill all of the space without gaps. The Bubble family (five-fold symmetries) encloses with an outside protective layer like an egg shell or a cell wall. The 'first egg' got its idea of structure from the interconnectedness of these two families.

These ideas grow out of the 12 spheres that begin layering in the closest-packed state. 12 spheres around our You/Me Ball create a 2BB VE (Sphere family). Take the central sphere out and the 12 spheres rearrange themselves into a 2BB icosahedron (Bubble family). One slight change and a whole new family of options comes into existence. This is the essence of any design you find in the natural world; a small effort creates surprising results.
Here you can see how you learn useful information when you reveal the equators of any system. The VE has a 60˚hexagon and the icosahedron has an undulating equator that is constructed out of 1/2 bubble diamonds. We know this is true because its color is orange. We know the 3 numerical constants of the bubble diamond's 90˚ triangle inside so we can calculate this measurements of these bubble triangles (1/2 bubble diamond).
