How to Build Mass Production Grids
Four Abilities of Self-Organizing Patterns
Self-stabilization
Self-correction
Self-regeneration
Self-innovation
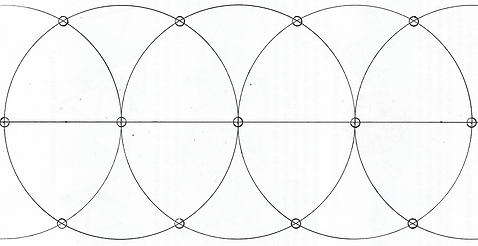
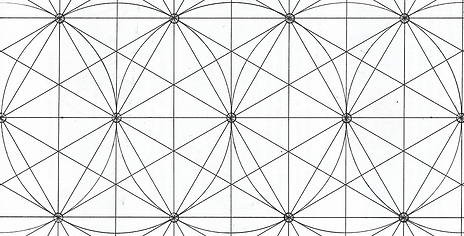
We discovered earlier in the tool box that the self-organization of circles produces the 60˚triangle grid. Out of this interconnectedness I developed a mass production grid for the other 4 "Not-Us" shapes.
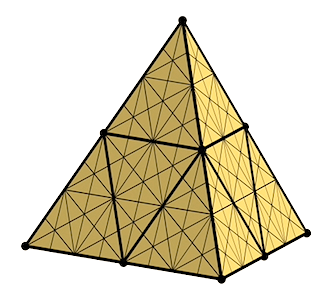
60˚Triangle Grid
for a 6BB Tetrahedron

If you will notice in the illustration above, each 60˚triangle is framed by a rectangle. This is the structure we need to build to mass produce 60˚triangles. We will call the horizontal length the 'when' measurement. The vertical one will be the 'where' measurement. Any grid for any shape will be begin with these two dimensions.
I use 6-ply railroad board (poster board) to build the geometrical models. Never trust an edge of your material to be square. At the bottom of your material draw a line close to the edge. From there, measure up to construct the 'where' lines up to the top. The when directions begins at a zero point somewhere near the edge on the left. Measure a 'when' length making sure there is enough distance to accommodate a protractor. Measure your 90˚ angle to construct the rest of the 'when' measurements. You now have your rectangular grid. Each shape connects locations-in-common in a unique way.
Where When
10.392304... 12
20.78 24
31.17 36
41.56 48
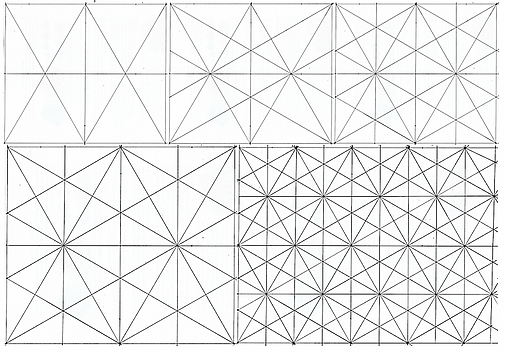
The 60˚triangle grid begins by framing any triangle with a rectangle. That is done by connecting opposite corners of two rectangles, one on top of the other.
This constructs the first triangles with some of them divided in half. There are two other ways to divide the edges of a 60˚triangle in half. The next series of lines of communication divides the edges and finds centers. This is the last ability of self-organization, self-innovation.
The first ability of self-organization is self-stabilization. Intersecting lines of communication define triangles which are the only self-stabilizing shape. If you have mis-measured the interconnecting of locations-in-common will self-correct any mistake. Self-reproduction is extended to the borders of the material. Defining the midpoint of the edges and the centers of each triangle is a self-innovation, very helpful in understanding the synergy of the grid.

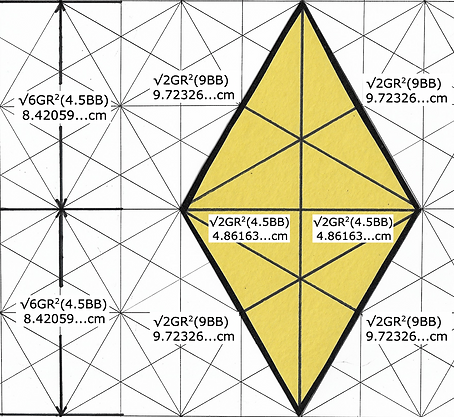
Where When
8.42095... 9.72326...
16.84 19.44
25.26 29.16
33.68 38.89
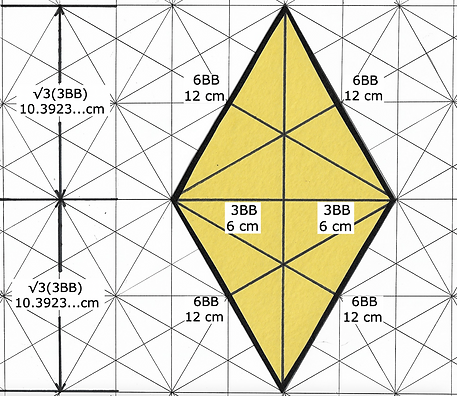
Layout for Sphere Diamond

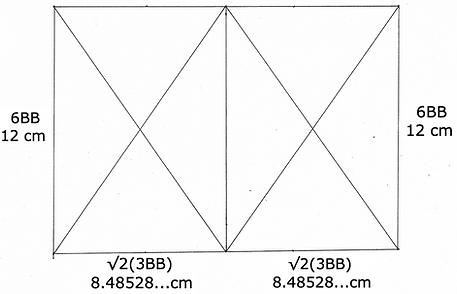
Where When
12 8.48528...
24 16.97
36 25.45
48 33.94
6BB = 12 cm
√2(3BB) = 8.48528...cm
√6(1.5BB) = 7.34846...cm
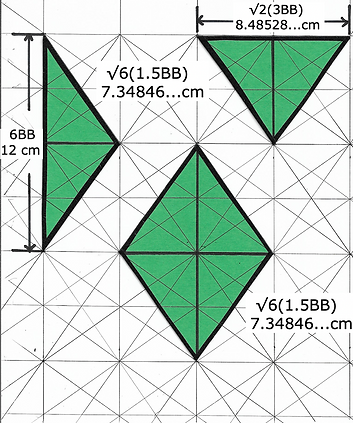

This grid is a little different. To not lose your way when drawing out this pattern remember it is a matter of connecting opposite corners of the various rectangles.The dividing in half here is supplemented by a series of 1/3 divisions that will prove helpful later.
Layout for Bubble Diamond


Where When
15.73258... 9.72326...
31.46 19.44
47.19 29.16
62.93 38.39
Layout for Square


Where/When
12
24
36
48
Here, the square's where/when measurements are the same. This is the only shape that has this unique characteristic.
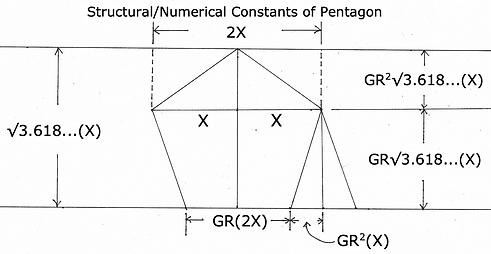

This dodeca's pentagon will be contained by the icosahedron when we interconnect them together like 'nesting dolls'. The edge the dodecahedron is √2GR(3BB) = 5.24419...cm. Newtools defines 1/2 of the long axis of the pentagon as 'X'. All other measurements will be relative to it.
Multiply the long axis by GR to get the edge. If you know the edge first, divide by GR. To find the altitude (how tall) multiply X by √3.618... The two divisions of the altitude are calculated by multiplying the altitude by GR and then that number by GR again. As far as I know, this information is unique to Newtools geometry.
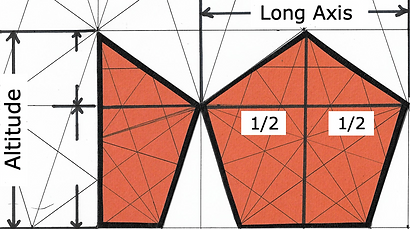


The grid for the pentagon is unique; it is a syncopated pattern, alternating tall and short rectangles.
These dimensions, 'Where', correspond to the GR divisions of the altitude. To maximize the use of space we will do a long-short-long as one cycle. If you want to fill up more space start another 3-part cycle.
Where When
(1/2 = 4.24264...cm)
4.98752... 8.48528...cm
+3.08398... 16.97
8.06988... 25.45
+4.98752... 33.94
13.0575... 42.42
The When direction is √2(3BB) = 8.48528...cm. We need to know the midpoint of this long axis of the pentagon. Draw out the full long axis on the grid. On the left side measure 1/2 of this length, √2(1.5BB) = 4.24264...cm. Then use the When lengths to find the rest of the midpoints.
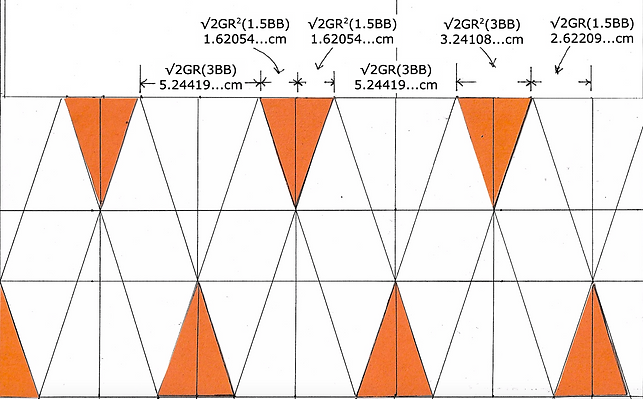
This grid uses what I call penta-cones. To mass produce the pentagon you need a space-filler companion to that shape. Pentagons alone did not fill all of the surface.
The cones are placed relative to the midpoint of the long axis. Using the half-measure of the edge or half-measure of the base of the cone, you map out their locations.
Once you have the marks around the midpoints of the long axis you begin to connect these locations-in-common. There is a pattern of small red cone--big clear cone--small red cone--big clear cone. You can see the beginning outline of the pentagon.
Edge of pentagon = √2GR(3BB) = 5.24419...cm
1/2 Edge of pentagon = √2GR(1.5BB) = 2.62209...cm
Base of penta-cone = (3BB) = 3.24108...cm
1/2 Base of penta-cone = (1.5BB) = 1.62054...cm

Now we begin to interconnect the lines of communication that exist in the pentagon. Think of this network as the corners of the red penta-cones talking with each other. If you have mis-measured, these alignments will self-correct. Once again, self-organization is not abstract but physical.
We now have drawn the five point star inside each pentagon. We need to finish out this cycle of self-organization by self-innovating. Now let's find the centers of each shape and divide the edges in half. we begin by connecting the bases of the penta-cones to each other.
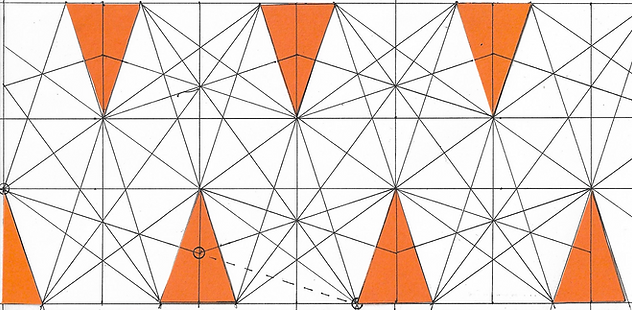
As with so much with this mass production grid, this next method of finding midpoints and centers is tricky. In the illustration you see a corner of a pentagon goes through its center, passes through a red penta-cone and interconnects with the corner another pentagon.
This continues the process of dividing the pentagon's edge in half. This is a variation of patterns we seen before of connecting corners of two shapes. Add the rest of the lines of communication necessary for each pentagon's edges are divided in half and all centers are confirmed.
To the best of my knowledge, this is the only mass production grid for a pentagon that produces this much exactitude. The self-organization of the pentagon gives us another example of the MEM (Most Effective Minimum) state of simple Design-in-Nature. This is the essence of
naturalmodular building techniques.

Another aspect of the pentagon that I never could find was the numerical constant that defined the center of a this shape.
After much trial and error I started using 'trail and error' meaning I looked to other patterns for clues. I eventually discovered the double division method.
Once again, the half-measure of the long axis provided the key. Take half the long axis divide it by √3.618... and then divide again by GR. That will give you the larger division of the altitude. Subtract that from the altitude to get the smaller measurement.
