90˚TRIANGLE FORMULA
PYTHAGOREAN THEOREM
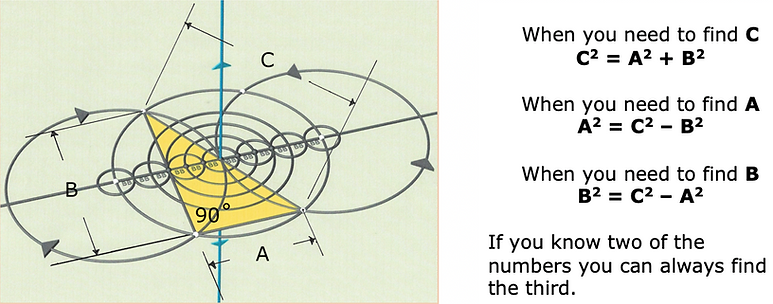
There are only 2 formulas in Newtools geometry, how to calculate the Golden Ratio and this formula. I call it the 90˚Triangle Formula because it is a more literal term.
If you know 2 measurements you can know the third. Above are the 3 different version to find the side you need.
This formula is very helpful when you want to confirm some BB numerical notation. Most structural situations in Newtools can be broken down into 90˚triangles. It also is a versatile tool when looking for patterns in unknown structures.
An icosahedron can be contained by an octahedron, meaning it fits exactly inside. Eight triangles of the icosahedron connect with the 8 triangles of the octahedron. There is a numerical constant that Newtools has found; = 0.540181513475453... Multiply this number with the edge and you get the length of the smaller triangle's edge. The edge of the larger triangle is divided into GR/ segments. You can use the 90˚triangle formula to confirm this.

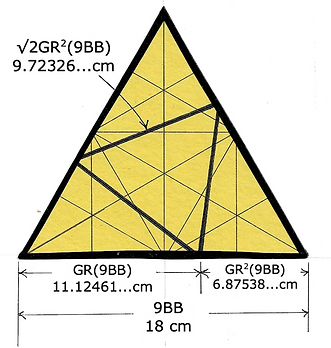
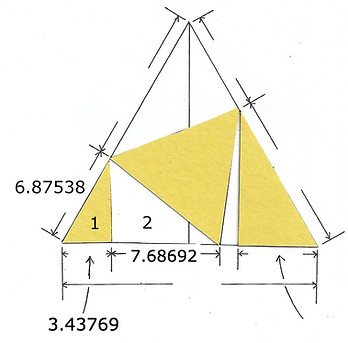

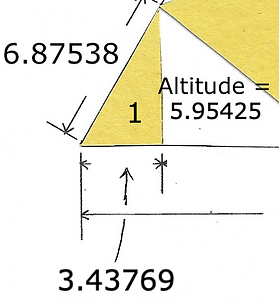

The color yellow tells a lot of useful information. We know each corner of the large triangle is 60˚. We can drop a perpendicular from the corners of the interior triangle to the base because we know whatever the hypotenuse's length (longest side) if we divide it in half at the base we will have a 90˚triangle. The constants of the yellow's 90˚triangle help us find measurements
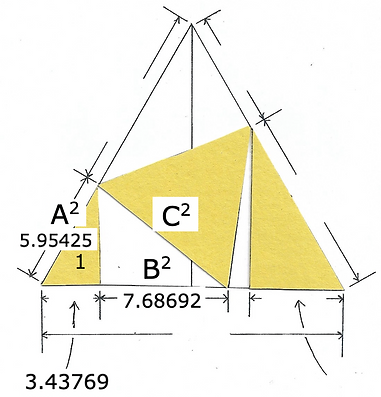


The 90˚Triangle Formula confirmed our constant between an icosahedron and an octahedron. The large numbers seem intimidating but they help us find our way in exploring fundamental structure. Rounding errors are a problem when doing these calculations. In the example above the two numbers are the same to 1/10 millionth of a millimeter, close enough for our purposes.
