Rhombic
Dodecahedron

Sphere Family Additions
Coupler

Hexagonal
Prism

Mothermod

Rhombic Dodecahedron


All of our new additions' sizes are relative to the 6BB VE and share at least six locations-in-common with the center of the square face of the VE (6 green map pins). The color green tells us the numerical constants of the sphere diamond's 90 degree triangle. With that information we know all of the other measurements (self-organizing).


Here is one of 12 symmetrical modular units of the r.dodeca. One side is the sphere diamond. The other 4 sides are a half-diamond we will call the sphere triangle. We will see this modular unit is 1/2 of a coupler, the next new system I will introduce.
Think Like a Sphere
Think Like a Rhombic Dodecahedron


We will shorten this name to r.dodeca. Rhombic means diamond shaped, do = 2, deca = 10, rhombic dodecahedron means a 12-sided diamond shaped system. It also can be thought of as a 12-sided sphere. The r.dodeca has all of the properties of a sphere but has flat sides. The closest packing of same-sized spheres and allspace-filling capacities become the same thing with the r.dodeca.
The 12 white directions pass through the center of the sphere diamond, the 8 blue directions on the 3-around outside corner, the 6 green directions in the 4-around outside corner and the 24 yellow directions divide the edge in 1/3-2/3 divisions.



The You/Me Ball can be contained by a r.dodeca with the long axis of its sphere diamond equal to 2BB = 4 cm. The 6BB long axis r.dodeca forms a containment field around the first layer of spheres. In the row of images below you see the center of the sphere defines the second layer of closest packed spheres, long axis of this r.dodeca = 8BB = 16 cm. The third layer constructs a 12BB = 24 cm long axis r.dodeca with the outside corner spheres of the VE are divided in half. All of this information is 'remembered'.

The rhombic dodecahedron fills allspace by itself with the same pattern spheres use to closest pack. When you see a sphere think r.dodeca. When you see a r.dodeca think sphere. This system has a deep connection to the other three systems we will introduce. The synergy of basic geometry is everywhere.

Structural Interconnectedness Between the
Rhombic Dodecahedron and the Bubble Family




The skeleton of the icosa (communication network between center and outside corners) is divided to interconnect with the r.dodeca. You will notice the GR/ segmenting of a length. This pattern is repeated over and over again. We can build the other connections of the r.dodeca with the Bubble family from the icosa.
There are 6 locations-in-common between the r.dodeca and the icosa that correspond to the 6 centers of the square faces of the cube that contains it. The 12 red directions are defined using the GR relationship.





All of the basic geometrical systems are interconnected with each other. The Newtools method of defining and measuring the synergy among parts allow you to develop a catalog of interconnectedness of modular building patterns.
The Coupler



Buckminster Fuller called this system the coupler because it connects with many other geometrical systems. There are two sizes we will explore, one size that is relative to the 6BB VE and the smaller size that is 1/6 of a 6BB long axis rhombic dodecahedron (r.dodeca).
A coupler is an asymmetrical octahedron (8 sides). Its size is determined by the length of its equator. The big one's equator is and the smaller is half that, 8.48528...cm.



Synergy Between Coupler and the Rhombic Dodecahedron

Inside any coupler is a half-sized r.dodeca. Inside any r.dodeca is 6 half-sized couplers. This is why each system fills allspace by themselves.
The 12 white directions in the coupler has 8 pass through the center of the sphere triangle and 4 through the 4 outside corners of the equator. The 8 blue directions are at the midpoint of the edge, the 6 green directions divided 4 at midpoint of equator and 2 at the polar caps. The 24 yellow directions divide the smaller sphere diamond's edge into 1/3-2/3 divisions.
Synergy Among R.dodeca, Coupler and the Cube



In another interconnection between the Sphere and Bubble family you see the same pattern of the cube inside the dodecahedron and the rhombic dodecahedron. The r.dodeca volume difference is a 1/2 coupler that is 1/6 of the volume of the cube. In fact if you turn the volume of a cube inside out around a cube of the same size you get a r.dodeca.
Variety of options is the basis of Design-in-Nature.



Synergy Among the Coupler, Tetrahedron, VE and Cube



We begin with what Fuller called the duo-tet, 2 tetras of the same size (12BB) sharing the same center, 'spinning' in opposite directions. The outside corners of this combination are locations-in-common with the outside corners of the cube of edge .
You can see by interconnecting the midpoints of the edge of the cube you define the equators of 3 large couplers with the same edge as the cube. The outside corners of the equators of these couplers share locations-in-common with the larger cube.



Structural Memory
The side effect of the communication networks that exist among the essential parts of a synergetic whole system is what I call structural memory. Once you understand an interconnected modular building pattern you can use that information in another building problem, you remember. My theory is the Design-in-Nature 'remembers' structural solutions in the same way, always available.
In this example, the tetra, coupler and cube define the outside protective layer around the 6BB VE. Four circles can define this VE or 14 sides. The 1/4 tetra sticking out from the VE give us an alternative structure for the cube.
Synergy Among the Rhombic Dodecahedron, Tetrahedron, Coupler, Cube and Octahedron



There are 14 outside corners of the r.dodeca. An internal structure within those corners can be constructed using an octahedron interpenetrated by a cube. There is an octa inside every r.dodeca. They fill allspace with a 1/4 tetra volume on each face of the octa. The duo-tet and tri-coupler combination forms the internal structure of the octa with the tetra sticking out with 1/4 volume.



The tetra, octa and r.dodeca share symmetric modular units, the 1/8 octa volume module and the 1/4 tetra volume module. Place the 1/8 octa mod on the four faces of a tetra and you construct a cube. Place the 1/4 tetra mod on the face of the octa and you construct a r.dodeca.



Inside any coupler is an octa. If you spilt that combo in half you get the modular building patterns of the cube with a VE inside of it. All of these combinations provide a variety of modular solutions to building problems.
Hexagonal Prism


The hexagonal prism and the mothermod are two special case modular systems. Neither are usually considered in any definition of basic geometry. I include them because they both are a large source of modular ideas.
We begin construction of the hexagonal prism with its side. You can see the rectangle is built around the 6BB long axis sphere diamond. The two additions are 1/3 of the sphere triangle, which is 1/2 of a sphere diamond. The edge of the top and bottom hexagon is 6.928203...cm.


The Synergy of the Rhombic Dodecahedron, Octahedron and Tetrahedron
Alignment of Axes of Spin
1/3 Division of Volume




We begin to define the interconnectedness by dividing the 6BB octa's volume into 1/3 units. The octa and tetra share the same axis of spin length, 9.79795...cm.
Next we divide the 6BB tetra into 1/3 volume units as well. With these units we can turn them inside out and the form the hexagonal prism.







Tetra and Octa with Rhombic Dodecahedron and the Hexagonal Prism



To understand the synergy (interconnectedness) between the r.dodeca and the hexagonal prism we need to know Fuller developed a smallest modular unit in the Sphere family he called the 'a'/'b' modules. There are 24 of the 'a' mods that make a 6BB tetra and 96 'a'/'b' mods that make an octa. 6 of these mods make 1/4 tetra volume and 8 make 1/3 tetra volume. We will go into detail about these units in the next section(section 'a', 'b', and 't' modules.)
Place a 1/3 tetra volume unit on each face of the octa and you have a hexagonal prism. Separate two 'a' mods at the top and hinge them onto the surface of the hexagon. Continue these process and you construct a rhombic dodecahedron.




Mothermod



This system is not listed in any geometry. Newtools includes it because it provides a wealth of modular options. A 'mother mod' is the volume difference between a 6BB VE and a 6BB octa divided into 8 symmetrical units. It 'remembers' how to interconnect many modular building patterns in both the Sphere and Bubble families.


The mothermod is constructed out of 6 1/2 squares and two equilateral 6BB triangles. There are many divisions that interconnect Sphere family systems.








One combination is the 3-1/4 couplers on top of a 1/4 tetra. In the photo, there are 6 'a' mods that define the 1/4 tetra. To define the 1/4 coupler there are 3 'a' mods and 3 'b' mods. Together they form a very interesting roof structure with plenty of areas for solar panel locations as well as providing a source of soft ambient light all day in this small house. There are surfaces the light bounces off of, passes through windows to be reflected on the dome-like ceiling. These two qualities, variety of options for placement of solar panels and soft ambient light all day are generally missing in most modular building designs. Naturalmodular emphasizes these qualities.



The 1/8 octa modular unit will prove very useful in solving many building problems. There is a half-sized mothermod inside any 1/8 octa. This forms a strong base for many ideas.






Inside any mothermod is a half-sized tetra/octa allspace-filling combination. There are 6 1/4 3BB octa modular units. This reveals a truncated dou-tet arrangement between two tetras left. At the heart of a 6BB mother mod is a 3BB octa.




Truncated Vector Equilibrium (VE)
This 26-sided geometrical system is part of the truncated family in the 20 most fundamental systems of Newtools geometry. It has special properties, one of them being it fills allspace with a 3-way interconnectedness with the tetra and cube. When thought of as modular building units it is very helpful.





Bubble Family Mothermod Units
Triacontahedron

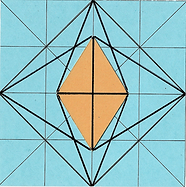



The edge of the dodeca is the same as the short axis of the bubble diamond 6.48217...cm. The edge of the icosa is the same as the long axis of the bubble diamond 10.48838...cm. The Golden Ratio divisions of the mothermod are the lines of communication between the outside corners of the bubble diamond and the outside corners of the square face of the VE (or midpoints of the cube that contains both.)
The 4 lines of communication from the long axis to the square edge is the same length as the altitude of the dodeca, 9.97504...cm. The short axis' 4 lines of communication are the same as the altitude of the icosa. Such simple symmetry and economy of means are typical of these patterns in Design-in-Nature.





Icosahedron Mothermod




Dodecahedron Mothermod




Icosidodecahedron Mothermod









The hexapod serves as an all-purpose first floor ceiling height standard of 3 meters. You multiply that number by √2 to get the edge of the hexapod. Dividing the edge by gives the alignment of the Bubble family systems.
