Octahedron As Outside Container

Another way of thinking about the interconnectedness of basic geometry is Buckminster Fuller's 'Jitterbug'. Using rubber tubing, you can make the outside corners of the VE a universal joint, meaning it can hinge in many different directions. The 24 outside edges of the VE can 'jitterbug' (transform) into an icosahedron, octahedron and tetrahedron all of the same edge length.

In this case, the edge of the octa is equal to the edge of the icosa in our nesting series, 9.72326...cm. I used the jitterbug relationship as the inspiration for this size.

Octahedron as Outside Container


Icosahedron Inside Octahedron

There are two types of modular units of this icosa inside an octa. The icosa is divided into 8 modular units and the volume difference between these two systems is defined by what Fuller called the 'S' module. Each corner of the octa is made up of 4 of these modules, 2 of them 'one hand', 2 of them other handed.


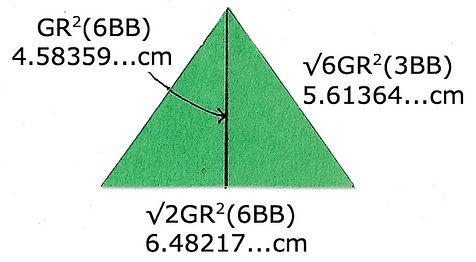
We begin by dividing the octa's triangle in the standard GR division.
We know the constant numerical value between the big and small triangle is 0.540181513475453... which produces a triangle of 5.25205...cm edge for the icosa.





The octahedron's skeleton (center/outside corner connection) is made of these blue triangles with long side 9.72326...cm. Divide that length by GR. The other 2 edges are divided by the standard GR division.








The 'S' modules always has a 'handedness', one turned 'inside-out' of the other. If you notice there is a logical interconnectedness among the measurements demonstrated by the You/Me BB measuring system developed by Newtools.
Dodecahedron Inside Octahedron


This model uses the octa's skeleton to orient the dodecahedron inside using the same blue triangle from the icosa. The small triangle to the right is a blowup of the triangle inside the original triangle giving you the outline of the internal pieces.



Knowing the numerical constants of the color blue allows us to find unknown numbers.
These modular units have a 'handedness' to them as well.




Cube Inside Octahedron






A different 1/3 division of the octa's triangle produces this modular piece. The rest of this unit is self-explanatory.


Tetrahedron Inside Octahedron




Tetrahedron

Octahedron