How to Define and Measure Structural Interconnectedness
Newtools has organized a set of structural and numerical constants that interconnect the fundamental structures of basic geometry into one synergetic whole system. To measure our simple expression of Design-in-Nature we will interconnect the "Not-Us" structural and numerical constants with our "You/Me" measuring system where all measurement is relative to our scale number and location.
Introduction to the Basic Tools
Four “Not-Us” Numerical Constants
These numbers act like the bases in our DNA, you will find them and their multiples in every measurement in Newtools geometry.
√2 = 1.41421356237095...
√3= 1.732050807568877...
GR = Golden Ratio = 0.618033988749895...
(What is important about this number is the 0.6180339... part which defines the "Fibonacci series". It is a convention to define it as a number between 1 and 2. I defined between 0 and 1 for easier calculation with my new measuring system.)
√3.618... = √3.618033988749895... = 1.902113032590307...
Six Basic “Not-Us” Shapes
Circles
The self-organization of circles gives birth to the other shapes.


You can think of the circle as the first word in the fundamental communication networks that interconnect basic building patterns. The first circle was actually the equator of the first sphere that reproduced its exact size to begin to pack together in Nature's Most Effective Minimum manner. In geometry this is called the closest packing of same-sized spheres. 'Closest-packed' means all of the centers of the spheres in the group are as close together as possible and they are touching as many other spheres as possible.
In the image above, you can see how 4 circles can self-organize to define a sphere. Each circle is in 60 degree orientation to each other and they form the 14-sided vector equilibrium (VE).


Circles can self-organize to produce a mass production grid of different shapes. Here it is for the 60 degree triangle. Draw a line across the middle of a sheet of paper. Choose a radius and draw a circle. Where the circle crosses the line is a 'location-in-common'. On that location draw another circle, continuing drawing circles to the other side.
You now have a series of locations-in-common that you can begin to construct 'lines of communication' between them. Each shape has a particular arrangement of connection. Here it produces a 60 degree triangle, diamond and hexagon.


As you continue to build out the communication network of the 60 degree grid two self-innovations happen. One, you find the center of each triangle and two, their edges are all divided in half. There seems to be a 'half-force' in Nature that repeats patterns on the half-scale and then the half-scale again. Some fractal patterns use this method. Building the half-size grid 'self-corrects' any mis-measurement you made originally. This is a visceral demonstration of Nature's self-organizing abilities.
Color Coordination of Shapes
5 Other "Not-Us" Shapes




Newtools gives each of these five shapes a color to organize the useful information inside each one. In the image above, it is easy to see which shapes that were used to construct the modular pieces of a cube surrounding the other 4 Platonic solids.
Each color represents a shape, "Not-Us" constant number or numbers, the angles of the shape and the always-the-same interrelationships in each shape's 90 degree triangle. These special case triangles are an example of minimum self-organization; if you know one measurement you know them all.
Yellow
60 Degree Triangle

The constant relationships among the 3 sides of each 90 degree triangle will always be relative to the base which will have the symbol X. This is the minimum definition of a self-organizing pattern, know one measurement you know them all.

Blue
Square


Red
Pentagon


Green
Sphere Diamond


Orange
Bubble Diamond


You/Me BB Measuring System
You/Me Ball = Regulation Ping Pong Ball


Our measuring system will begin by combining you and me into one local observer. We can do that by choosing a sphere that will be our You/Me Ball. I chose a regulation ping pong ball because the International Federation of Table Tennis oversees the manufacturing of tournament balls insuring that all are the same size, radius = 2 cm (centimeters). Our measuring system is based on the ability of same-sized spheres to 'closest-pack' meaning their centers are the closest possible and all spheres are touching the maximum number of another spheres.
I define this 2 cm radius as our BB (Bellybutton) measurement. Like our navels are a 'cut-off knot' from all genetics before us and represents the beginning of our independent existence, our BB is a 'cut-off number' from all measurement before and starts a new way of measuring structure. This BB = 2 cm becomes our scale number and the center of this first sphere becomes our all-purpose location-in-common.
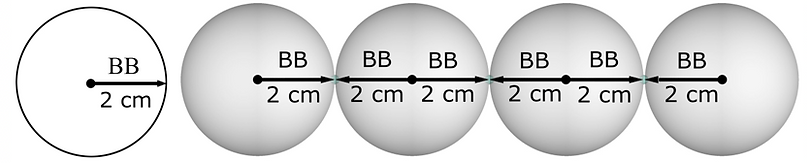
When you measure distance with spheres you measure from center-of-sphere to center-of-sphere. The length defined by 4 spheres is 6 radii or 6BB = 12 cm. We will use this 6BB = 12 cm as the maximum reach of the influence of our You/Me ball. Any number bigger will be multiples of this number. This size-relativity-limit is based on one of the most basic structural/numerical constants, how spheres of the same size group together in a Most Effective Minimum arrangement.
We now have the basic components for any measurement in Newtools. Each will have some combination of the 4 "Not-Us" numbers or their multiples combined with our BB scale number or their multiples. This gives us a 'genealogy' of the calculations that made each mathematical notation. In the 2. Guide to the Basic Tools portal I go over this same material in much more detail.
Most Effective Minimum State (MEM)
How to Do More By Using Less
Naturalmodular building techniques are based on two fundamental assumptions. The first one is thinking and building like Nature in its simplest form starts with the structural and numerical constants you find that exist in Nature (basic geometry). The second assumption, according to my theory, is the 'do more/use less' design aesthetic in Nature strives to achieve the Most Effective Minimum (MEM) state.
Most effective means an efficient balance between choice and usefulness. There is a wide variety of methods that Nature uses to build structures. Variety coupled with sustainability could be a definition of minimum usefulness. Sustainability grows out of the minimum state which begins with four characteristics.
Most economical in use of materials and space
Least effort to realize and replicate
Most accommodating to change
A measuring system that connects the individual to the synergetic whole system
The You/Me BB measuring system grows out of the ability of same-sized spheres to pack together in a Most Effective Minimum arrangement.
The Closest Packing of Same-Sized Spheres

We are going to use Buckminster Fuller's theory about the closest packing of spheres. There are several other theories but Fuller's is based on the triangle which is the only self-stabilizing shape found in Nature. His arrangement of spheres produces a new geometrical system (polyhedron) to combine with the Five Platonic Solids; the 14-sided Vector Equilibrium (cuboctahedron).



According to Fuller's theory, there are three layers in the first cycle of spherical growth. With our chosen You/Me Ball defining the BB = 2 cm size, the maximum reach of our center is 6BB =12 cm.
A VE (vector equilibrium) has 14 sides, 8-60 degree triangles and 6 squares. Fuller states this is as close as we can get to a balanced state in structure. The lines of communication from the center to the outside corners are equal to the lines of communication the outside corners have with each other.
The layering process begins by asking a question, "What is the minimum number of spheres that will surround our You/Me Ball in a MEM arrangement? The answer is 12 spheres. The distance between centers is 2BB = 4 cm. You can define the communication network that exists between the center of our You/Me Ball and the centers of this outside layer spheres with 4 circles in 60 degree orientation to each other. They show the 2BB distance from the center out to the outside corners and the 2BB distance between corners.



Our scale number is BB = 2 cm, this radius of our You/Me Ball.


The first layer of 12 spheres around 1 has a distance between centers of 2BB = 4 cm.


The second layer is 42 spheres around 12 around 1. The distance is 4BB = 8 cm.



The third layer is 92 spheres around 42 around 12 around 1. The maximum distance in this first cycle of initial growth is 6BB = 12 cm. Bigger numbers will be relative to this number.


Sphere-Speak

When you divide these 146 spheres around 1 in half a hexagon is reveal. Here you see all of the different ways a hexagon can express itself. It is the universal translator of 'sphere-speak'.


The primordial (at the beginning) language of the communication networks in this geometry is sphere speak. The first word was 'circle', which was the equator of the 'first sphere'. The sphere began to replicate exact copies of itself and discovered how to 'closest-pack'. This spherical constant is the foundation of our You/Me BB measuring system.
