Guide to Basic Tool Box
Glossary
"What's meant let that be said"
Naturalmodular Building Techniques
These building techniques grew out of the ordering of the useful information in Newtools geometry. It is my theory that basic geometry provides a whole new palette of modular building options embedded in the simplest of structures. What is needed is a method of defining, measuring, mapping and building physical models of the structural and numerical constants that interconnect these modular patterns into one synergetic whole system.
In my opinion, naturalmodular defines one of the Most Effective Minimum (MEM) expression of Design-in-Nature. At the beginning, this website will limit our exploration to the simplest, most 'regular' polyhedra (geometrical systems) found in basic geometry, the Five Platonic Solids, with the 14-sided vector equilibrium (VE) added later as our mapping outer boundary. All of the practical advantages of Newtools and naturalmodular can be found in these simplest of structures.
Most Effective Minimum (MEM) State
Effectiveness in Nature is a practical balance between choice and usefulness. When you look to the natural world for building ideas you discover a wide variety of methods to do the same thing; evolution is about individual choice. Variety coupled with sustainability could define a basic usefulness. Sustainability grows out of the minimum state which has four basic characteristics.
Most economical in the use of material and space
Least effort to realize and replicate
Most accommodating to change
A measuring system that connects the individual to the bigger whole system
Design-in-Nature
Design-in-Nature is a vast area with a multitude of options. Relative to Newtools geometry, I will define it in a very limited context using the simplest structures in geometry. Design-in-Nature is any building pattern that achieves maximum structural integrity with a minimum investment in material, space or effort. To find these patterns you must develop whole systems thinking where you look for the connections between the parts of the whole. Whole systems thinking will lead you to doing more by using less.
Structural Integrity
Structural integrity is the interconnectedness of the parts of a structure. When a load is placed on one part, the stress is 'communicated' over the whole of the structure providing greater strength. Maximum expression of structural integrity has synergy.
Synergetic Whole Systems
Synergy is the behavior of whole systems unpredicted by the behavior of the parts taken individually. These systems will always to more than the sum of their parts because of the communication networks that exist among their integral parts. An integral is a part essential for the completion of the whole. Each integral 'knows' its exact relationship with every other integral, change one and the rest will change in unison to maintain a constant interrelationship. These constant relationships among integrals are the foundation of naturalmodular's self-organizing building patterns.
Self-Organizing Building Patterns
Simple self-organizing patterns can be recognized by understanding how structural and numerical constants are ordered. Newtools' tool kit catalogs the 4 numerical and 6 structural constants that define our self-organizing patterns. The simplest definition of a self-organizing pattern is if you know one measurement, you know them all.

Geometrical Systems
Traditionally, the structures of basic geometry have been called polyhedra. Buckminster Fuller suggested 'system' was much more of a realistic description. In Newtools, a geometrical system is a container that divides our local environment into three easy-to-describe physical states:
Inside the system
Outside the system
The thickness of the system itself
This definition emphasizes the physical nature of the structures of basic geometry.
Containers
Geometrical systems are containers. Containers have the ability to organize their integral parts by developing lines of communication from any center to all of the fundamental locations-in-common on their outside limits. There are four fundamental locations-in-common:
1) Center of the geometrical system
2) Outside corners and the lines of communication between them (edges)
3) Symmetric division of the edge (1/2, 1/3, GR)
4) Center of outside shape (face)



What is Fundamental?


Whole systems thinking allows you to interconnect fundamental structures into one synergetic whole where one system fits inside another exactly.
Newtools defines 20 geometrical systems as fundamental. They were chosen to demonstrate the wide variety of interconnectedness that exists among the integrals of individual systems as well as how all of the 20 form one synergetic whole system. Some are traditionally described as fundamental while several were chosen for their interesting modular design.
Two Job Description Families of Basic Geometry
Sphere Family (Allspace-filling)

Traditionally, these systems have been called allspace-filling. I named them the Sphere family because of the deep connection allspice-filling has with the sphere. When stacked together, these systems occupy all of the space with no gaps between them. Some can do this by themselves, some with a partner and a few with a 3-way interconnectedness. In Newtools, 15 of the fundamental 20 are allspace-filling.

Cube
The cube can fill allspace by itself.
Tetra/Octa
There is a half-size order in systems that fill allspace. Here the half-sized systems build the same sized tetra as above.

Duo-Tet
Two tetras can form the outside corners of a cube. The 8 outside corners of these two tetras share the same locations as the outside corners of the cube.
Tetra/Octa
The tetra and octa work in combination to fill allspace. Whichever system you begin with place the other on each face and they will fill without gaps. Continue this process for bigger arrays.

Tetra/Octa
This same combination of half-sized tetras/octas produces an octa. These two systems are two of the most fundamental structures in Nature.

This system is included to show a 3-way allspace-filling combination. The tetra, cube and truncated rhombic dodecahedron fill all of the space.
Bubble Family (Five-Fold Symmetries)

I call this the Bubble family because a bubble has a thin outside layer. These systems have traditionally been called the 'five-fold symmetries' because the number five is prominent in the construction of these structures.
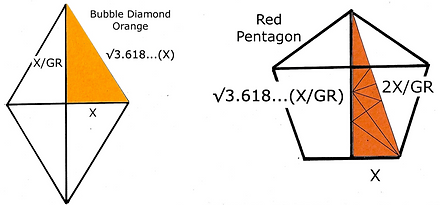
The job description of the Bubble family is to enclose with an outside protective layer like an egg shell or a cell wall. Only these systems have the measurements GR (Golden Ratio) = 0.618033988749895... and √3.618... = √3.618033988749895... = 1.902113032590307... If you see these number or their multiples you know they are in the Bubble family.
