VE and Bubble Family Hexapod
Bubble Family and the Hexapod

The edge of the VE that is the container around the Bubble family is 6BB = 12 cm. In this section we will use the four systems of the Bubble family as domes over the first floor hexapods.
There are two characteristics that will be emphasized. One, multiple surfaces to place solar panels to increase collection of light. Two, creating multiple surfaces for light to bounce off of, pass through a window and reflect on the interior of the dome-like ceilings.
Triacontahedron Inside 6BB VE

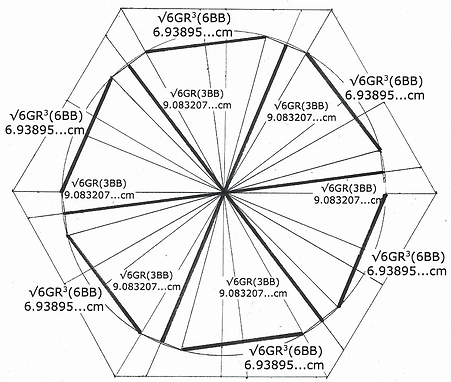
To orient the triaconta's equator divide the edges of the 6BB hexagon by multiples of GR.

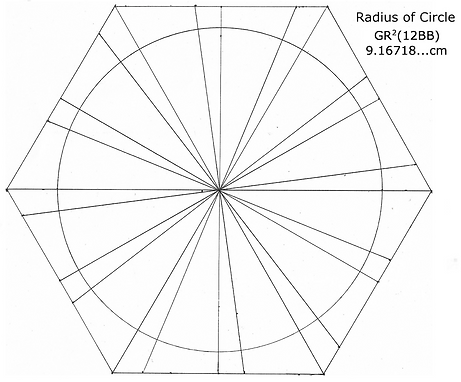
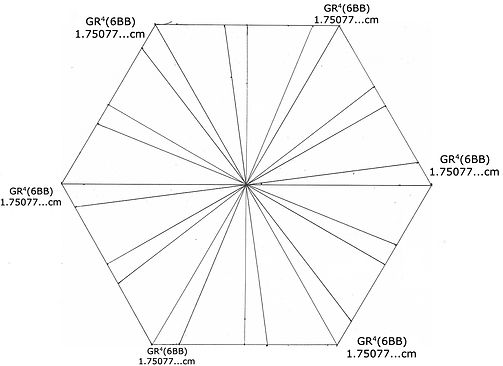
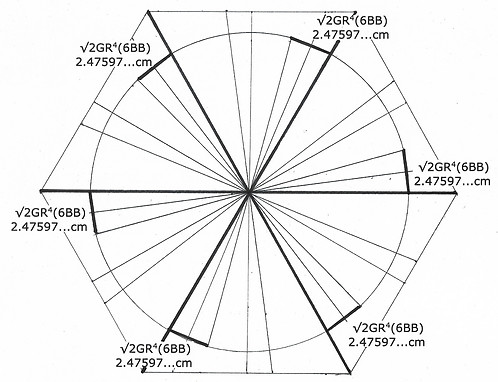
The maximum limit of the equator of the triacontahedron that fits inside a 6BB VE is 9.16718...cm. Draw a circle with this radius to locate the limit. On this outside limit measure 2.47597...cm over from the edges of the hexagon's triangles to get the small dimension of the equator. The midpoint, 1.23798...cm connects with the 1.75077...cm division of the hexagon. This produces these cone-like shapes with edges of 9.16718/2.47597...cm. Connect the corners of these cones and you have the 6.93895...cm side of the equator.




I see my job as laying out the details of how to build a certain structure and then developing 'push-off-start' ideas of how these structures might by developed into a modular building system.
By developing a system where rectangular windows can be placed within these triangular pieces in a Most Effective Minimum manner will keep the costs down.
This view will be facing south in the northern hemisphere and north in the southern hemisphere. As the sun comes up the early morning light will hit the dome. As it raises the structure blocks any direct light inside allowing only reflected light to illuminate the dome is a soft ambient light that lasts all day.
Icosahedron Inside 6BB VE


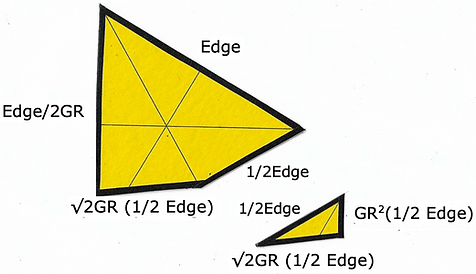
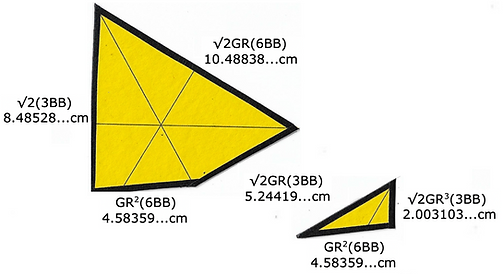
We first slice the icosa's triangle to accommodate the equator. There is a 'handedness' to these pieces. Tape two triangles together, measure 8.48528...cm along their shared edge to get an exact cut.

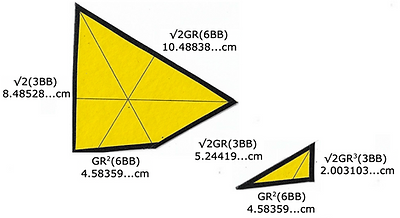
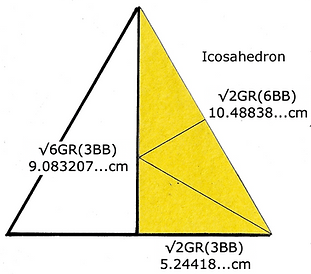

You divided the 6BB hexagon with the same GR multiples as the triaconta's equator. There are 2 lines of communication between the center and the outside limit. In this example, the one connected to the 1.75077...cm division will always be the altitude of the icosa's triangle, 9.083207...cm. The second will always be the truncated edge of the triangle that accommodates the equator, 8.48528...cm.


Dodecahedron Inside 6BB VE




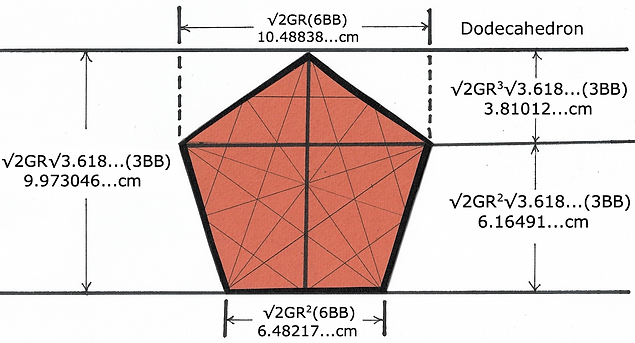



Here is an idea for the dodeca that uses an extension on top of the axis of spin corner. This model is attempt to maximize the reflected light while providing multiple areas for solar panels. The photo on the left shows the interior window unit to capture reflected light.
All of these examples are 'push-off start' ideas that need an architect or engineer to explore their practicality.
Icosidodecahedron Inside 6BB VE




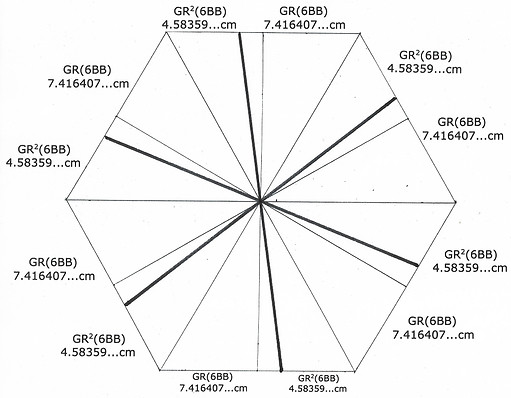
This modular building idea for the icosidodecahedron uses the information from the circle organization of the interconnectedness between the icosidodeca and the VE. In portal 5 under Intro/ Bubble Family are the measurements and layouts for this organization of the volume inside.
Equator of Icosidodeca


The equator for the icosidodeca is the same as the dodeca's. The 6BB hexagonal equator of the VE is divided using the standard GR division. The 8.48528 cm edge of the icosidodeca's equator is the same division as of the dodeca as well.
