Most Effective Minimum Expression of
In-All-Directions-All-At-Once
12 Spheres

We learned in the Basic Tool Box Guide that 12 spheres can define the two fundamental structural job description families; Sphere family (allspace-filing) that when stacked fill all of the space without gaps and the Bubble family (five-fold symmetries) that enclose with an outside protective layer like an egg shell or cell wall.
12 spheres around our central You/Me Ball constructs a 2BB-edge VE. If we take the central ball out the 12 spheres self-organize into a 2BB icosahedron. Revealing their equators shows the internal alignment. A very small change provides an abundance of useful information. From this information I decided that this model was a simpler method of mapping the communication networks connecting any center to it outside limits.
98 Directions
50 Sphere Family Directions
62 Bubble Family Directions
14 Directions-in-Common

50 VE (Sphere Family) Directions
12 White Directions
From center through centers of spheres
8 Blue Directions
From center to center of triangle-shaped gap
6 Green Directions
From center to center of square-shaped gap
24 Yellow Directions
From center through tangent (kissing) location

62 Icosahedron (Bubble Family) Directions
12 Red Directions
From center through centers of spheres
20 Blue Directions
From center to center of triangle-shaped gap
30 Green Directions
From center through tangent (kissing) location
14 Directions-in-Common Between the Two Families
8 Blue Directions
6 Green Directions
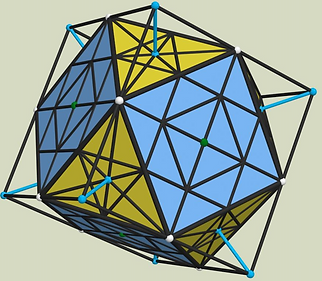

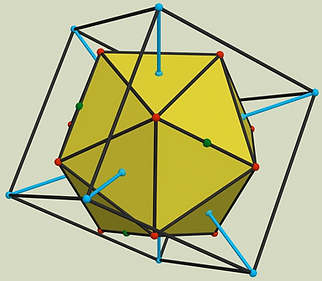
Once again, there is a simple symmetry that interconnects these two basic families of structure. Most often they are taught separately with Fuller being one of the first to connect them. Newtools and naturalmodular places their synergy is at the core of this structural order.
The 12 white directions connect the VE's center to its outside corners. In the cube these directions are the midpoint on its edge. The 12 red directions connect the icosahedron's center to its outside corners. In the cube, if you connect 2 white directions you have a line that divides the square face in half. When this length (same as edge) is multiplied by GR = (0.61803398874...) you have the distance between the 12 red directions on this mid-line.
These 8 blue and 6 green directions will always appear in both structural families. This helps you align and contain systems inside each other. Contain means one system fits exactly inside another like the icosahedron inside the cube and/or the VE (vector equilibrium).
